Don’t be afraid to use “tricks” on the SAT!

To do well on the SAT, you need to know a good bit of mathematics. And when you understand math deeply, you also begin to understand all kinds of interesting “tricks”, or shortcuts, that you can apply to SAT-style math questions. Many of these shortcuts are actually pretty clever and interesting in their own right, and demand that you have a mature understanding of the questions you are dealing with. You might be surprised just how many fabulous shortcuts there are, just waiting for you to use them! Of course, it all depends on the type of question you’re confronted with. In this blog, we’ll be looking at some angle problems.

Figuring out a shortcut: what’s given? what isn’t?

Consider the following geometry problem about angle measures.

Question:  Find the value of x \(+\) y \(+\) z in the diagram below.

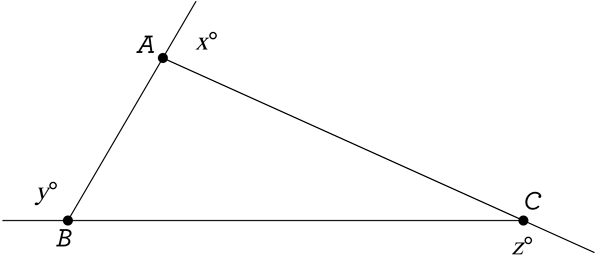
A. 180\(^\circ\)

B. 270\(^\circ\)

C. 360\(^\circ\)

D. 540\(^\circ\)

Notice what we have given: a triangle ABC, with 3 exterior angles, each formed when a side of the triangle is extended. The measures of these exterior angles in degrees are x, y, and z, and we need to find the value of their sum. You might try to eyeball the answer somehow, but at times you will be told these pictures are “not drawn to scale”, which basically means they are deliberately not drawing the diagram the way it should really look. So now what?

Well, dig a little deeper into what is given, and what isn’t given. You are given a triangle, but you not given any special information about it. It could be any type of triangle: acute, scalene, right, isosceles, equilateral, whatever. So the fact that they are even asking you this question, and not specifying what kind of triangle is given, means that x \(+\) y \(+\) z must be the same number no matter what kind of triangle you’re looking at! In other words, for any triangle you could possibly draw, the sum of the measures of each exterior angle, x \(+\) y \(+\) z, is definitely one of the numbers in that list of answer choices! How can we use this information to our advantage?

Shortcut: imagine the “best” possible shape!

Now that we realize x \(+\) y \(+\) z is always going to be the same number, no matter what type of triangle is given, all we have to do is imagine the best possible triangle to think about! Usually, the “best” object is the simplest, the least difficult, the most understandable. Here, the best triangle would be… equilateral! That’s because know lots of things about equilateral triangles, including their angle measures: all 60 degrees! Let’s redraw the picture, but for when ABC is equilateral:

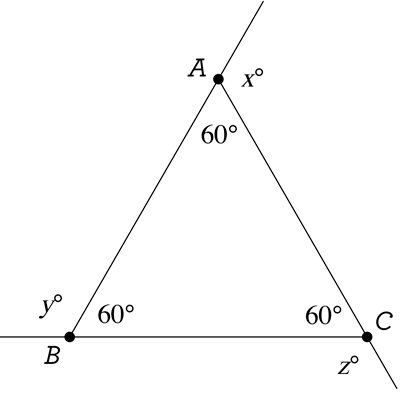
Whatever the value of x \(+\) y \(+\) z is here, that’s the value it will always be, for every other triangle. And here we can easily calculate our sum, because we can calculate every unknown angle measure! For example, x \(+\) 60 \(=\) 180, because we have two angles forming a “straight angle”. Therefore x \(=\) 120, and the same goes for y and z:

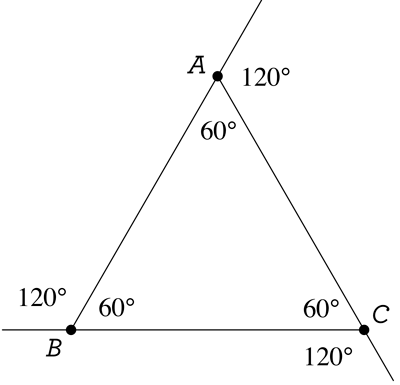
Now we’re done: x \(+\) y \(+\) z \(=\) 120 \(+\) 120 \(+\) 120 \(=\) 360, and the answer must be C.

Clever, right? And notice that this shortcut actually does require some deep understanding of the question, in both content and style. Never feel ashamed that you’re using a shortcut… be proud that you understand so much!

Now a problem for you to practice

Armed with our new shortcut, try this next problem yourself. And don’t scroll down too far, or you’ll accidentally see the answer too soon!

Question: Find the value of w \(+\) x \(+\) y \(+\) z in the diagram below.

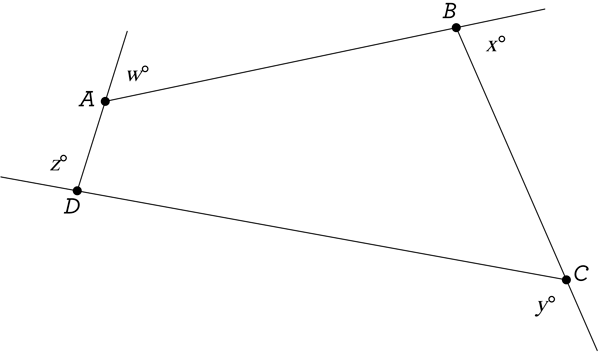
A. 180\(^\circ\)

B. 270\(^\circ\)

C. 360\(^\circ\)

D. 540\(^\circ\)

And the answer is...

...360\(^\circ\) once more! You are given a quadrilateral ABCD with four exterior angles, and you wish to find the sum of their measures. Just like before, since the question implies that w \(+\) x \(+\) y \(+\) z is always going to be the same value no matter what the shape of ABCD is, why not pick the “best” shape, one that we know plenty about: a rectangle!