A Single Picture can Explain the Pythagorean Theorem

What the Pythagorean theorem says
There are hundreds upon hundreds of proofs of the Pythagorean Theorem, and they all tell you why the Theorem is true, using all kinds of different techniques. Some of the best proofs, in our opinion, are the ones that consist of a single, simple picture. And that’s because a picture proof makes the explanation “bite-sized”, something that sticks in your mind, allowing you to recall that proof much faster than, say, a 10-line proof involving similar triangles (for more on pictures and retention, see our blog here). Let’s recall what the Pythagorean Theorem says: if you have a right triangle of side lengths a, b, and c, where c is the length of the side across from the right angle, then it’s definitely true that a2 + b2 = c2. (Remember a and b are the “leg” lengths, and c is the length of the “hypotenuse”.) More briefly, the Theorem says:
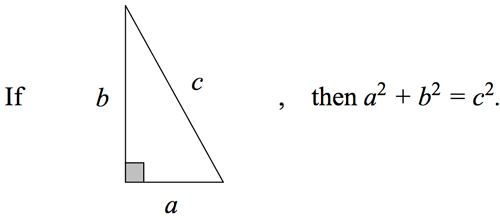
The Pythagorean Theorem rephrased… using area!
Now, if you look at our “Pythagorean equation” a2 + b2 = c2, you see three numbers being squared. In order to get to our picture proof, we need to interpret everything through pictures. Well, squared numbers make us think of… squares, and area! In particular, a2 is the area of a square of side length a. Likewise, b2 is the area of a square of side length b, and c2 is the area of a square of side length c. Hmm… we would like to see these squares; where should we put them? We could just put them on the sides of our right triangle! Let’s be creative and see where it leads us!
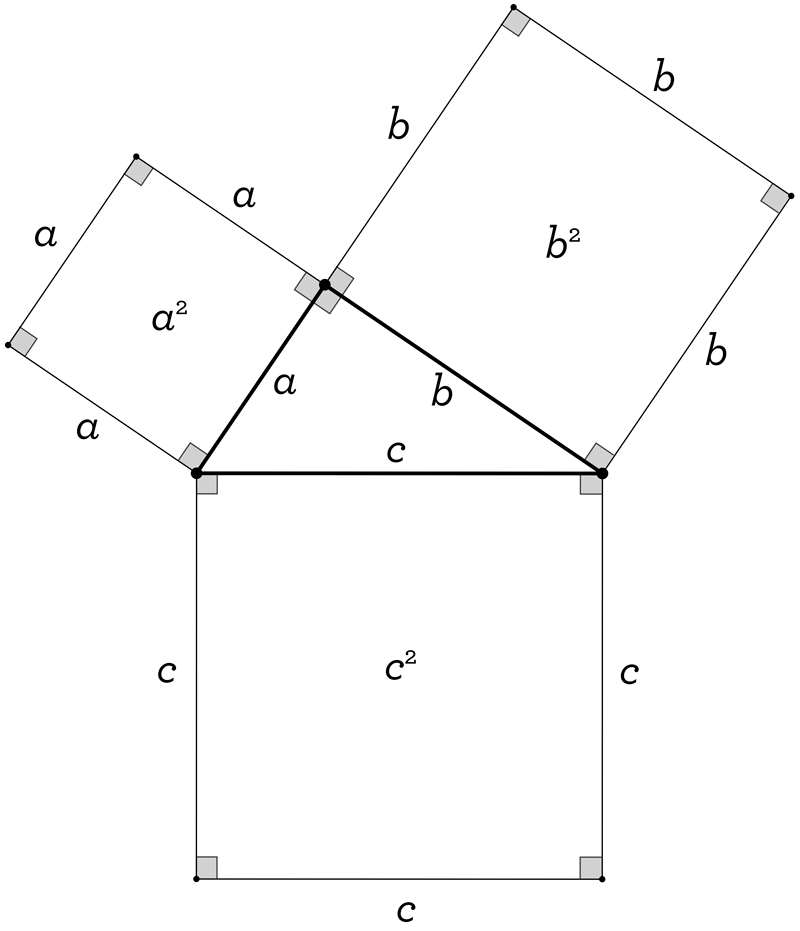
Again, given our right triangle, the Theorem tells us that a2 + b2 = c2. But now that we have our picture with squares inserted, we can use this to reframe the equation in terms of area. Looking at our above picture, the Theorem is telling us that the combined area of the squares on the legs of our right triangle (a2 + b2) is equal to the area of the square on its hypotenuse (c2).
Using area as a tool to provide the proof
Well then, we have recast the Pythagorean Theorem as a theorem about area. Interesting, but is it useful? It is! We can use our picture above to prove the theorem! Are you ready? Here’s the proof:
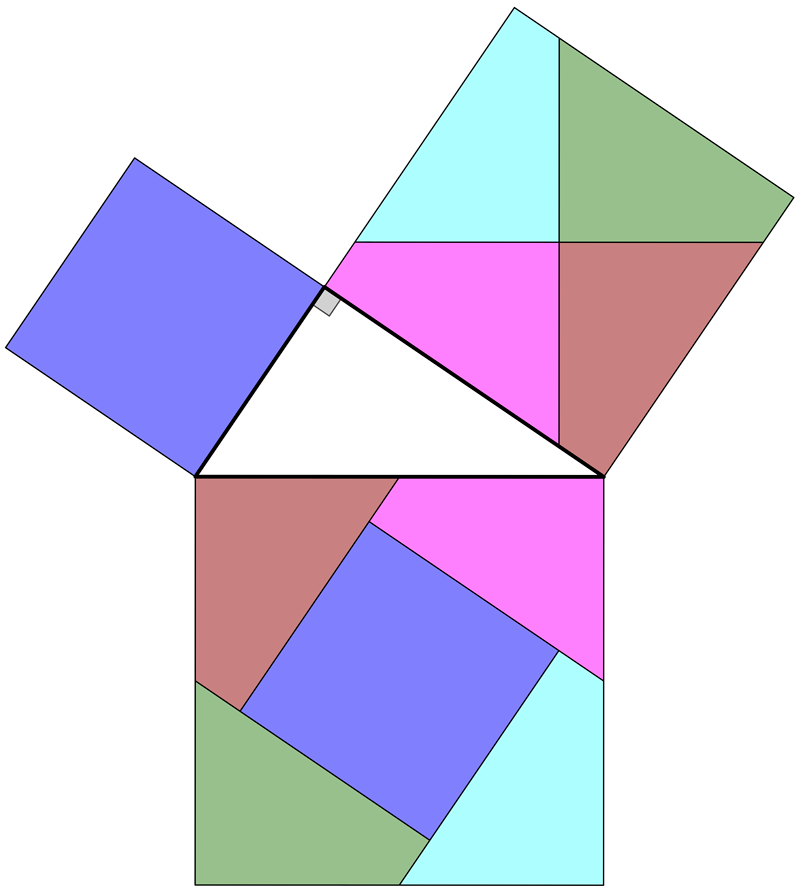
Do you see why this explains that a2 + b2 = c2 is true for a right triangle? We need to understand that the combined area of the two top squares is really just the area of the bottom square. But that’s exactly what the picture is showing you! If you leave one of the top squares alone, and cut the other into 4 identical pieces, you can rearrange them so that they all snugly fit in the bottom square. You can see this (and the colors are there to help you see how the pieces are rearranged). And when you see it, you understand why the theorem is true! And it’s so easy to remember!
This proof was found by a man named Henry Perigal, in the 1800’s; this diagram is on his tombstone. Who wouldn’t want to be remembered for such a clever and pretty proof!
What kind of proof is this?
This proof is known as a “dissection proof”, since it involves cutting one of the squares into smaller pieces (we have a blog on that too, here). But the larger issue here is that it is a proof by picture, also called a “proof without words”, since there aren’t any words in it! We love picture proofs, and our current Problem deals with a lovely proof without words. We like them because they are artful, and manage to convey so much information in so small a space. When you see it, and think about it, you get it, and when you get it, you won’t forget it.

Details, details…
There are a few things here that you might be wondering about. “I get the proof, it’s sweet, but… how do you know where to make those cuts? And how do you know, really know, that those five pieces up top really do fit perfectly into the square on the hypotenuse?” Ah, all great questions. And those details really do need to be carefully explained to make this proof complete. The required explanations can definitely be worked out, and we encourage you to do so. But for now, let’s just gaze upon this picture, and appreciate how slick mathematics can truly be!
Did you find this blog interesting? Follow this blog using the links above to get other useful ideas from exSTEMsions delivered right to your inbox!
Want awesome tips and a mini-challenge, all designed to help you build vital problem-solving and critical thinking skills in your child? Click here to sign up for our monthly newsletter!



