Mathematicians are everywhere...

A common misperception about math is that if you’re good at it, then doing math must be your calling. Nothing could be further from the truth. Many people are fabulous at math; some go on to become mathematicians and physicists, and some don’t. In fact, it’s possible to enjoy math just like anything else we might enjoy, like painting, or basketball, as a hobby. There are all kinds of people who do math, but don’t do it for a living, including a some very famous people! So, this is the first of a series of blogs to fill you in on some of the famous historical figures that didn’t shy away from math.

A recent problem concerned a cool theorem in geometry that you could discover simply by drawing with drinking glasses. So, it seems fitting that the first historical figure in our series should have a geometry theorem named after him: Napoleon.

One of the most famous European leaders of all time, Napoleon was the emperor of France in the early 1800’s, and conquered a vast empire across Europe. Napoleon is considered by some to be a terrible tyrant, and by others to be a military genius; but as this is not a history blog, we will only briefly consider him as a geometer.

Was it really Napoleon's theorem?

Unfortunately, the history behind the geometry nugget known as Napoleon’s Theorem is spotty at best. What we know is that the theorem we’re going to show you was named after him, and that’s about it. Did Napoleon really create it? If he did, when? Nobody knows. Many think that Napoleon didn’t actually come up with this theorem, because… well, c’mon, it’s Napoleon. But it is known that Napoleon did converse with some of the leading mathematicians of his day, and even spoke with them about geometry; yes, it seems that Napoleon really did enjoy math! Whether or not you think Napoleon’s Theorem really is Napoleon’s, we hope you think it’s at least pretty cool anyway.

What is Napoleon's Theorem?

In order to tell you what Napoleon’s Theorem is, we need to get some vocabulary out of the way first. This theorem is all about triangles, and equilateral triangles play a big part. An equilateral triangle is a triangle with all sides having the same length. As you might remember, an equilateral triangle is therefore highly symmetric; that means that there is a point right in the very “middle” of the triangle, called its center. Below is an equilateral triangle, and its center is the red point.

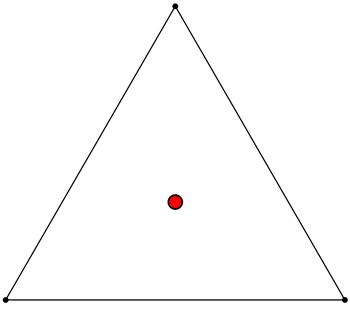
(If you have an equilateral triangle in front of you, you can find its center by folding it in half through one of its vertices, and then folding it in half again through some other vertex. The two creases of your folds will intersect at its center! And if you want your triangle to be nice and flat, there’s no need to fold; just draw where the creases would be!)

Now we have all the ingredients we need for Napoleon’s Theorem. Start off with a triangle ABC, of any shape and size:

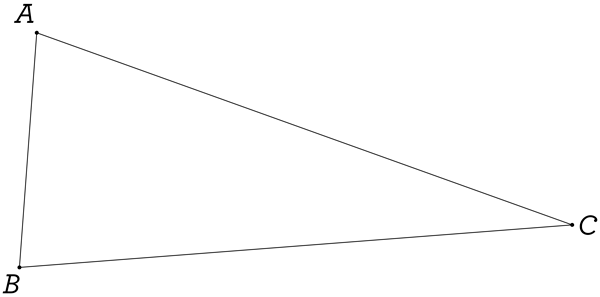
Now, construct an equilateral triangle on each of its sides. In other words, for each side of our triangle, we make that segment one of the sides of an equilateral triangle! Each of these three new equilateral triangles should be projected away from our starting triangle ABC, or “outwardly”. When you do that, you should mark the center of each equilateral triangle (ours are colored blue).

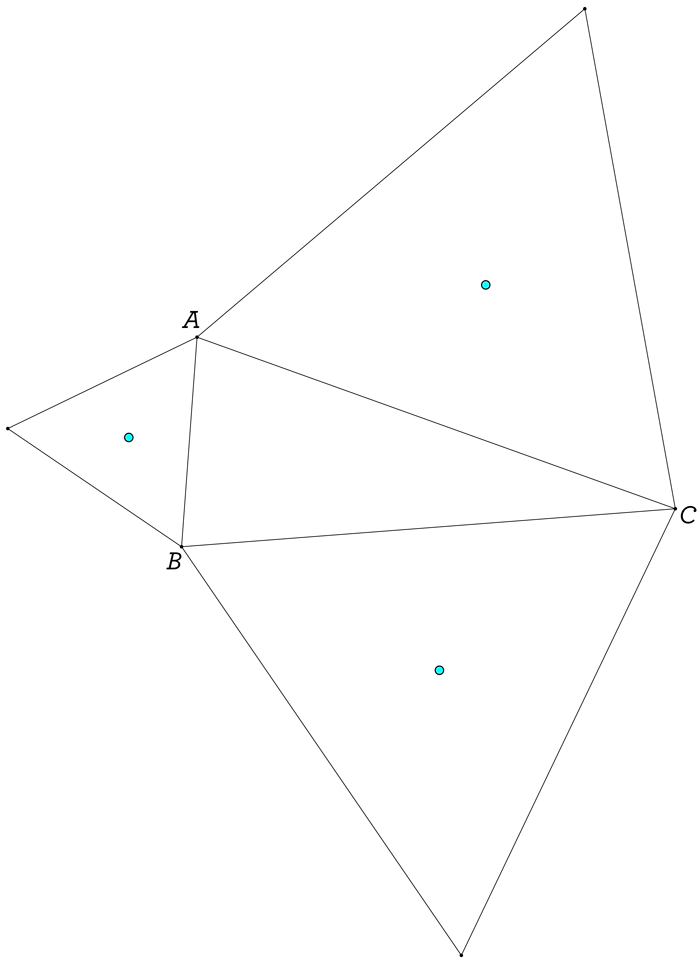
What do you notice about those three blue points? Think about it for a little bit, before you look at our next diagram, where we draw the triangle that those blue points create. In other words, we’re about to update the diagram to show you the triangle formed by the centers of those equilateral triangles. Brace yourself:

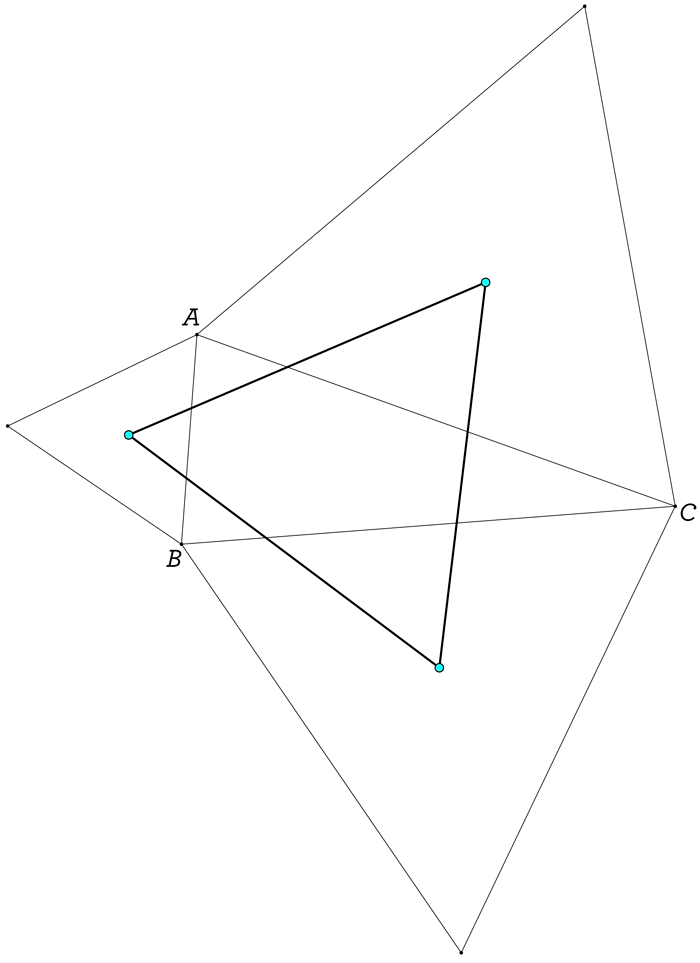
Did you see it? The centers of those equilateral triangles form another equilateral triangle! And this always works, no matter what our original triangle ABC looks like! Very cool. Shall we summarize?

Napoleon’s Theorem: When equilateral triangles are constructed outwardly on the sides of a given triangle, the centers of those equilateral triangles form yet another equilateral triangle!

Try it for yourself!

And now, a challenge for you. Draw a triangle ABC, and try to carefully draw three equilateral triangles, one on each side of ABC, but this time draw them inwardly. In other words, the three equilateral triangles you draw will overlap ABC. Draw the triangle created from the centers of these equilateral triangles, just like we did above. If you’ve done this carefully, you’ll notice something really cool. Don’t see it? Email us at [email protected] and we’ll send you the answer! You can also message us on Facebook or Instagram @exstemsionslearning.

If you found this blog interesting we've got more to share! Follow this blog using the link at the top of the page!

Want awesome tips and a mini-challenge, all designed to help you build vital problem-solving and critical thinking skills in your child? Click here to sign up for our monthly newsletter!

Looking for other ways to hook your kids into math, maybe with a story about a castle and a king? Try Moat from our TpT Store!