There’s math in your television!

Given that most people don’t particularly want to think about math when they’re relaxing and watching their favorite TV show, you won’t find much mathematics on the television. But math does pop up from time to time, even in popular shows. Occasionally, there’s actually a lovely math story lurking behind an episode of a favorite program! As we will see, even Homer Simpson takes a stab at mathematics, which leads us to revisit a very famous geometry theorem, and then dive into some higher-level thinking when we examine what Homer’s really saying!

Homer the mathematician

There’s a fun episode of the Simpsons (season 5, episode 10) where Homer puts on a pair of glasses he finds in a public bathroom, and with newfound super-smartness, proclaims the following:

“The sum of the square roots of any two sides of an isosceles triangle is equal to the square root of the remaining side.”

Someone offscreen promptly tries to corrects him:

“That’s a right triangle, you idiot!”

A cute scene, but we math people are dying to know: who’s right? Does Homer know what he’s talking about, or not?

The Pythagorean Theorem to the rescue

It sounds like Homer is trying to recite the Pythagorean Theorem, but flubs it, since that theorem only applies to right triangles, as the anonymous person pointed out to him. But to see what’s really going on here, we should first remind ourselves what the Pythagorean Theorem actually says. We have a whole blog on it here, but here’s the quick rundown. Without mincing too many words, the Pythagorean Theorem says:

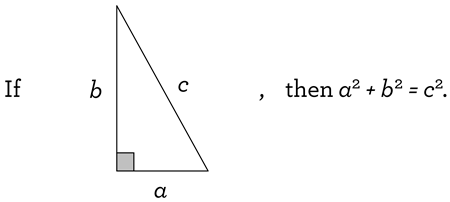
Basically, if you have a right triangle, then there is a nifty equation involving the lengths of the triangle’s sides. Remember that c is the length of the “hypotenuse”, and a and b represent the lengths of the “legs”. With this language, we can write the Theorem in one nice sentence, a sentence that sounds vaguely similar to Homer’s proclamation:

“The sum of the squares of the leg lengths of a right triangle is equal to the square of the length of its hypotenuse.”

Of course, as it seems Homer was trying to recite this Theorem, we now know that there are other errors in his statement besides missing the right triangle part. For one thing, the Pythagorean Theorem doesn’t deal with square roots of side lengths, it deals with their squares. For another, the Theorem doesn’t say that we can sum the squares of any two sides; we have to sum the squares of the legs to have anything fabulous happen.

If Homer and the person who corrected him were trying to recite the Pythagorean Theorem, they were both off by a long shot!

Okay, it’s not the Pythagorean Theorem, but it is true anyway?

And now, in our math brains, a question arises: Homer wasn’t correctly stating the Pythagorean theorem, but was he stating a theorem nonetheless? Maybe Homer is giving us some other strange theorem that nobody’s ever heard of! In other words, the real question here is: is his statement true or false? And let’s ask a very general question, and not worry if the triangle is isosceles or right:

Is it ever possible to have the sum of the square roots of two sides of a triangle be equal to the square root of the remaining side?

Unfortunately for Homer, the answer is an emphatic NO. One of the ways we can see such a triangle isn’t possible, is to assume that it is possible, and find a contradiction, a totally false and nonsensical statement. If assuming it is possible leads to a falsehood, then we were wrong to think it was possible in the first place! (Never seen a proof by contradiction before? We explain what they are here.) In other words, if we assume that there is a triangle where the sum of the square roots of two side lengths is equal to the square root of the length of the remaining side, we can arrive at a contradiction, which will mean that no such triangle could ever exist.

And here’s the proof, to put your curious mind at ease!

So, we start off by assuming that there IS a triangle, say with side lengths a, b, and c, where the square roots of two of those sides add up to the square root of the third side, like so: $$\sqrt{a}+\sqrt{b}=\sqrt{c}$$

Now, we are going to figure out that this assumption leads us to a contradiction, which will tell us that we never should have assumed that such a triangle exists, in which case Homer, and the person who corrected him, are sadly incorrect.

The key to our contradiction is the following very simple statement:

For any two positive numbers \(a\) and \(b\), \(\sqrt{a+b}<\sqrt{a}+\sqrt{b}\).

In other words, as long as you are dealing with two positive numbers, the square root of their sum is always less than the sum of their square roots. (You can prove this any number of ways, for example, with algebra. For now, just convince yourself this statement is reasonable by plugging in some numbers!)

So, here’s what we know. We are starting with our assumption that for triangle side lengths a, b, and c, we have$$\sqrt{a}+\sqrt{b}=\sqrt{c}$$

But our new tool tells us $$\sqrt{a+b}<\sqrt{a}+\sqrt{b}$$Since the right hand side of that inequality is actually just \(\sqrt{c}\), make a substitution to get: $$\sqrt{a+b}<\sqrt{c}$$If you remember your inequalities, we can now square both sides to arrive at: $$a+b<c$$

And this is a contradiction! The above equations tells us that two sides of our triangle have total length less than the third side, which tells us that our triangle couldn’t possibly exist! Indeed, for a triangle to exist, the total length of any two sides must be bigger than the length of the third side (something known as the Triangle Inequality), otherwise there isn’t enough length to form a closed three-sided figure! Thus there is no triangle with side lengths satisfying \(\sqrt{a}+\sqrt{b}=\sqrt{c}\), as it leads to a contradiction. Done!

Afterthought: why did Homer say what he said?

We think Homer was trying to remember the Pythagorean Theorem. So, why are there so many errors in Homer’s statement? As it turns out, the writers were simply referencing the well-known Wizard of Oz movie. Homer was repeating, word for word, what the Scarecrow said when he finally “got a brain”. Homer even had the same pose that the Scarecrow had in that movie!

If you watched the Wizard of Oz before you saw that episode of the Simpsons, then you might be pleasantly surprised at the reference!

Find this post interesting? Follow the blog using the link at the top of the page to get notified when new posts appear!

Want awesome tips and a mini-challenge, all designed to help you build vital problem-solving and critical thinking skills in your child? Click here to sign up for our monthly newsletter!