What the Pythagorean Theorem isn’t

Ask a friend what the Pythagorean Theorem is. Everybody thinks they know it. It’s the one theorem in mathematics that everyone is seemingly familiar with, and can rattle off immediately. Most people say that the Pythagorean Theorem is simply this:

$$a^2+b^2=c^2$$

However, this is most certainly NOT the Pythagorean Theorem. Don’t get angry, this is the fun of mathematics! We learn. Learning is fun. Stay with us here.

Which of course leads us to… proverbs!

Do you remember these three famous sayings?

The tough get going.

But prepare for the worst.

Don’t fix it.

No? But they do ring a bell, don’t they? These are only parts of famous proverbs; the second parts, to be exact. Those three lines above are not complete proverbs, but these are:

When the going gets tough, the tough get going.

Hope for the best, but prepare for the worst.

If it ain’t broke, don’t fix it.

The second part of the saying doesn’t make too much sense without the first part! Much is the same with mathematical sayings. When someone says that the Pythagorean Theorem is a² + b² = c², I always ask: “What are these values a, b, and c? Are they three sides of a hexagon? Are they negative numbers?” That equation is nifty, but by itself, there is no context that tells you what anything there actually means. What do the values a, b, and c represent? If you don’t tell me that, then that equation doesn’t mean much of anything! In fact, the equation is only the second part of the Theorem.

What the Pythagorean Theorem is

The equation a² + b² = c², by itself, is not enough information to tell you what the Theorem is really trying to say; the numbers a, b, and c need some context for everything to make sense. The needed context is that a and b are the lengths of the legs of a right triangle, and c is the length of its hypotenuse. (Remember, the hypotenuse of a right triangle is the side opposite the right angle.) So, what the Theorem is telling you is this: if you see a right triangle with the side across from the right angle having length c, and the other two sides having lengths a and b, then certainly a² + b² = c². That is the full statement of the theorem, with the given information up front, and the conclusion afterwards. Or, if you’d like to see things written as succinctly as possible:

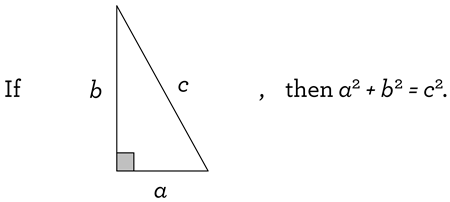
The above picture/statement shows you the context of the concluding equation, by showing you where the values a, b, and c come from; without this, the equation isn’t meaningful. That means that a² + b² = c², by itself, is not the Pythagorean Theorem. If you like, you can call a² + b² = c² the Pythagorean Conclusion, since it appears at the end of the Theorem. Even better, you can call a² + b² = c² the Pythagorean Equation, since it is, indeed, an equation. But a² + b² = c² is only part of the Theorem; if you’re missing the front part, you’re missing out on what the theorem really is!

Find this post interesting? Follow the blog using the link at the top of the page to get notified when new posts appear!

Want to actually put some of your family's geometry skills to work? Check out our newest addition to our TpT store, Circles!

Want awesome tips and a mini-challenge, all designed to help you build vital problem-solving and critical thinking skills in your child? Click here to sign up for our monthly newsletter!